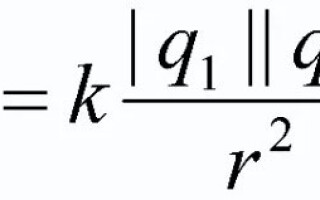חוק קולומב, הגדרה ונוסחה - מטענים חשמליים ואינטראקציה ביניהם

בין גופים טעונים יש כוח אינטראקציה שבזכותו הם יכולים למשוך או להדוף אחד את השני. חוק קולומב מתאר כוח זה, מראה את מידת פעולתו, בהתאם לגודל וצורת הגוף עצמו. חוק פיזיקלי זה יידון במאמר זה.

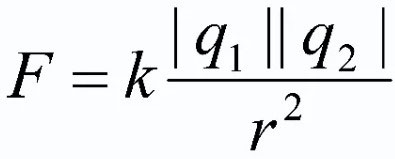
נוסחת החוק של קולומב.

תוֹכֶן

1 טעינות נקודתיות נייחות
2 מאזן פיתול של צ'ארלס קולומב
3 גורם מידתיות k וקבוע חשמלי
4 כיוון כוח הקולומב והצורה הווקטורית של הנוסחה
5 איפה חוק קולומב מיושם בפועל
6 כיוון הכוחות בחוק קולומב
7 היסטוריה של גילוי החוק

טעינות נקודתיות נייחות

חוק קולומב חל על גופים נייחים שקטנים בהרבה ממרחקם מחפצים אחרים. מטען חשמלי נקודתי מרוכז בגופים כאלה. בעת פתרון בעיות פיזיות, ממדי הגופים הנחשבים מוזנחים, כי הם לא באמת חשובים.

בפועל, מטענים נקודתיים במנוחה מתוארים באופן הבא:

נקודה מטען חיובי q1. נקודה מטען חיובי q2.

במקרה זה ש₁ ו-q₂ - זה חִיוּבִי מטענים חשמליים, וכוח הקולומב פועל עליהם (לא מוצג באיור). הגודל של תכונות נקודתיות אינו משנה.

הערה! מטענים במנוחה ממוקמים במרחק נתון זה מזה, אשר בבעיות מסומן בדרך כלל באות r. בהמשך המאמר, חיובים אלו יישקלו בחלל ריק.

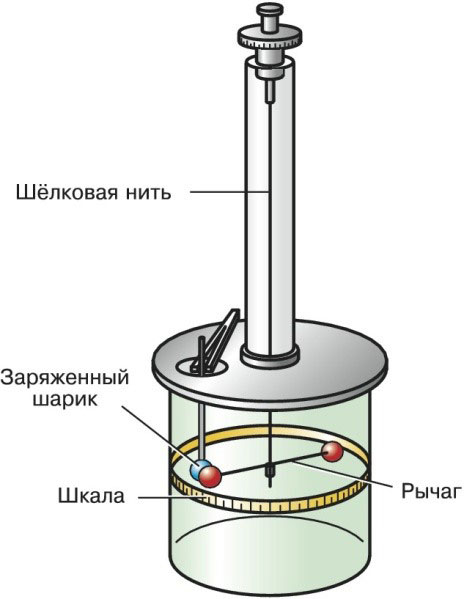
מאזן פיתול של צ'ארלס קולומב

מכשיר זה, שפותח על ידי קולומב בשנת 1777, עזר להסיק את התלות של הכוח שנקרא מאוחר יותר על שמו. בעזרתו נחקרת האינטראקציה של מטענים נקודתיים, כמו גם קטבים מגנטיים.

למאזן פיתול יש חוט משי קטן הממוקם במישור אנכי שממנו תלויה מנוף מאוזן. מטענים נקודתיים ממוקמים בקצות הידית.

תחת פעולת כוחות חיצוניים, הידית מתחילה לנוע אופקית. הידית תנוע במישור עד שיאוזן בכוח האלסטי של החוט.

בתהליך התנועה, המנוף סוטה מהציר האנכי בזווית מסוימת. זה נלקח כ-d ונקרא זווית הסיבוב. לדעת את הערך של פרמטר זה, ניתן למצוא את המומנט של הכוחות העולים.

קרא גם: מהו זרם חשמלי במילים פשוטות

מאזן הפיתול של צ'רלס קולומב נראה כך:

מאזן פיתול של צ'ארלס קולומב.

גורם מידתיות k וקבוע חשמלי 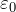$\varepsilon_0$

בנוסחה של חוק קולומב ישנם פרמטרים k - מקדם המידתיות או $\varepsilon_0$ הוא הקבוע החשמלי. קבוע חשמלי $\varepsilon_0$ מוצג בספרי עיון רבים, ספרי לימוד, באינטרנט, ואין צורך לספור אותו! גורם מידתיות ואקום מבוסס על $\varepsilon_0$ ניתן למצוא לפי הנוסחה הידועה:

$k = \frac {1}{4\cdot \pi\cdot \varepsilon_0}$

כאן $\varepsilon_0=8.85\cdot 10^{-12} \frac {C^2}{H\cdot m^2}$ הוא הקבוע החשמלי,

$\pi=3.14$ - פאי,

$k=9\cdot 10^{9} \frac {H\cdot m^2}{C^2}$ הוא מקדם המידתיות בוואקום.

מידע נוסף! מבלי לדעת את הפרמטרים שהוצגו לעיל, לא יעבוד למצוא את כוח האינטראקציה בין מטענים חשמליים שני נקודתיים.
ניסוח ונוסחה של חוק קולומב

לסיכום האמור לעיל, יש צורך לתת את הניסוח הרשמי של החוק העיקרי של אלקטרוסטטיקה. זה לוקח את הצורה:

כוח האינטראקציה של שני מטענים נקודתיים במנוחה בוואקום עומד ביחס ישר למכפלת המטענים הללו וביחס הפוך לריבוע המרחק ביניהם. יתר על כן, את תוצר החיובים יש לקחת מודולו!

$F=k\cdot \frac {|q_1|\cdot |q_2|}{r^2}$

בנוסחה זו ש₁ ו-q₂הם האשמות נקודתיות, נחשבות לגופים; ר² - המרחק במישור בין הגופים הללו, שנלקח בריבוע; k הוא מקדם המידתיות ( $9\cdot 10^{9} \frac {H\cdot m^2}{C^2}$ עבור ואקום).

כיוון כוח הקולומב והצורה הווקטורית של הנוסחה

להבנה מלאה של הנוסחה, ניתן לדמיין את חוק קולומב:

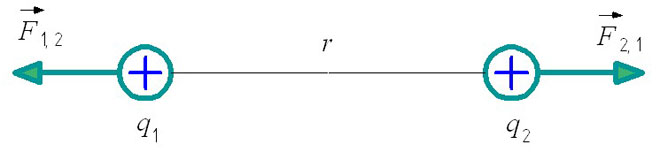
כיוון כוח הקולומב עבור שני מטענים נקודתיים באותה קוטביות.

ו_1,2- כוח האינטראקציה של המטען הראשון ביחס לשני.

ו_2,1- כוח האינטראקציה של המטען השני ביחס לראשון.

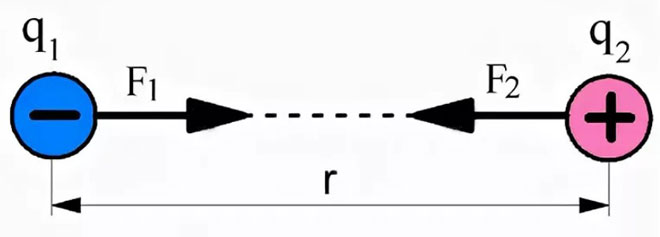
כמו כן, בעת פתרון בעיות של אלקטרוסטטיקה, יש צורך לקחת בחשבון כלל חשוב: מטענים חשמליים בעלי אותו שם דוחים, ומטענים מנוגדים מושכים. מיקום כוחות האינטראקציה באיור תלוי בכך.

אם נחשבים מטענים מנוגדים, אזי כוחות האינטראקציה שלהם יופנו זה אל זה, תוך תיאור משיכתם.

כיוון כוח הקולומב עבור שני מטענים נקודתיים בעלי קוטביות שונה.

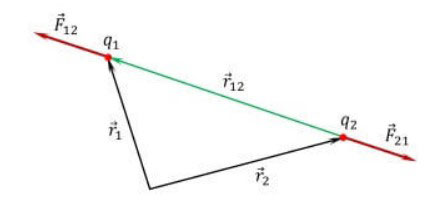
הנוסחה של החוק הבסיסי של אלקטרוסטטיקה בצורה וקטורית יכולה להיות מיוצגת באופן הבא:

$\vec F_1_2=\frac {1}{4\cdot \pi\cdot \varepsilon_0}\cdot \frac {q_1\cdot q_2}{r_1_2^3}\cdot \vec r_1_2$

$\vec F_1_2$ הוא הכוח הפועל על המטען הנקודתי q1, מהצד של המטען q2,

$\vec r_1_2$ הוא וקטור הרדיוס המחבר את המטען q2 עם המטען q1,

קרא גם: איך להכין מעגל מודפס אלקטרוני בבית?

$r=|\vec r_1_2|$

חָשׁוּב! לאחר כתיבת הנוסחה בצורה וקטורית, יהיה צורך להקרין את כוחות האינטראקציה של מטענים חשמליים בשתי נקודות על הציר כדי לשים את הסימנים בצורה נכונה. פעולה זו היא פורמליות ולעיתים מבוצעת באופן נפשי ללא כל הערות.

איפה חוק קולומב מיושם בפועל

החוק הבסיסי של האלקטרוסטטיקה הוא התגלית החשובה ביותר של צ'ארלס קולומב, שמצא את יישומו בתחומים רבים.

יצירותיו של הפיזיקאי המפורסם שימשו בתהליך המצאת מכשירים, מכשירים, מכשירים שונים. למשל, מטה ברק.

בעזרת מקל ברק מוגנים מבני מגורים ומבנים מפני ברקים בעת סופת רעמים. לפיכך, מידת ההגנה על ציוד חשמלי מוגברת.

מטה הברקים פועל על פי העיקרון הבא: בזמן סופת רעמים מתחילים להצטבר בהדרגה מטענים עזים של אינדוקציה על הקרקע, שעולים למעלה ונמשכים אל העננים. במקרה זה, שדה חשמלי גדול למדי נוצר על הקרקע. בסמוך למוט הברקים מתחזק השדה החשמלי, ובגלל זה נדלק מטען חשמלי קורונה מקצה המכשיר.

יתרה מכך, המטען הנוצר על הקרקע מתחיל להימשך למטען הענן עם הסימן ההפוך, כפי שצריך להיות על פי חוק צ'ארלס קולומב. לאחר מכן, האוויר עובר תהליך של יינון, ועוצמת השדה החשמלי פוחתת בסמוך לקצה מטה הברקים. לפיכך, הסיכון לחדירת ברק לבניין הוא מינימלי.

הערה! אם הבניין שעליו מותקן הברק נפגע, אז לא תהיה אש, וכל האנרגיה תיכנס לאדמה.

בהתבסס על חוק קולומב פותח מכשיר בשם "מאיץ החלקיקים" אשר מבוקש מאוד כיום.

במכשיר זה נוצר שדה חשמלי חזק, המגביר את אנרגיית החלקיקים הנופלים לתוכו.

כיוון הכוחות בחוק קולומב

כפי שהוזכר לעיל, כיוון כוחות האינטראקציה של מטענים חשמליים שתי נקודות תלוי בקוטביות שלהם. הָהֵן. מטענים בעלי אותו שם ידחו, ומטענים של מטענים מנוגדים ימשכו.

קרא גם: איך להכין גלאי מתכות במו ידיך, עזרה למתחילים

כוחות קולומב יכולים להיקרא גם וקטור הרדיוס, מכיוון הם מכוונים לאורך הקו שנמתח ביניהם.

בחלק מהבעיות הפיזיקליות, ניתנים גופים בעלי צורה מורכבת, אשר לא ניתן לקחת עבור מטען חשמלי נקודתי, כלומר. להתעלם מגודלו. במצב זה יש לחלק את הגוף הנדון למספר חלקים קטנים ולחשב כל חלק בנפרד, באמצעות חוק קולומב.

וקטורי הכוח המתקבלים בפיצול מסוכמים לפי כללי האלגברה והגיאומטריה. התוצאה היא הכוח המתקבל, שיהווה את התשובה לבעיה זו. שיטת פתרון זו נקראת לרוב שיטת המשולש.

הכיוון של וקטורי הכוח של קולומב.

היסטוריה של גילוי החוק

האינטראקציות של שני האשמות נקודתיות לפי החוק הנחשב לעיל הוכחו לראשונה בשנת 1785 על ידי צ'ארלס קולומב. הפיזיקאי הצליח להוכיח את אמיתות החוק המנוסח באמצעות מאזני פיתול, שעקרון פעולתו הוצג גם במאמר.

קולומב גם הוכיח שאין מטען חשמלי בתוך קבל כדורי. אז הוא הגיע להצהרה שניתן לשנות את גודל הכוחות האלקטרוסטטיים על ידי שינוי המרחק בין הגופים הנבדקים.

לפיכך, חוק קולומב הוא עדיין החוק החשוב ביותר של האלקטרוסטטיקה, שעל בסיסו התגלו רבות מהתגליות הגדולות ביותר. במסגרת מאמר זה הוצג הנוסח הרשמי של החוק וכן תוארו בהרחבה חלקיו המרכיבים אותו.

מאמרים דומים: