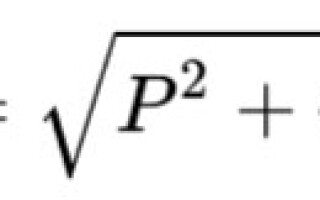כולנו נתקלים בכל יום במכשירי חשמל, נראה שהחיים שלנו נעצרים בלעדיהם. וכל אחד מהם בהוראות הטכניות מציין את הכוח. היום נבין מה זה, נלמד את סוגי ושיטות החישוב.
תוֹכֶן
מתח במעגל זרם חילופין
מכשירי חשמל המחוברים לרשת פועלים במעגל זרם חילופין, ולכן נשקול את ההספק בתנאים אלו. עם זאת, ראשית, בואו ניתן הגדרה כללית של המושג.
כּוֹחַ - כמות פיזיקלית המשקפת את קצב ההמרה או ההעברה של אנרגיה חשמלית.
במובן צר יותר אומרים שהספק חשמלי הוא היחס בין העבודה שבוצעה על פני פרק זמן מסוים לפרק זמן זה.
אם לנסח את ההגדרה הזו בצורה פחות מדעית, מסתבר שכוח הוא כמות מסוימת של אנרגיה שנצרכת על ידי הצרכן לאורך תקופה מסוימת. הדוגמה הפשוטה ביותר היא מנורת ליבון רגילה. הקצב שבו נורה ממירה את החשמל שהיא צורכת לחום ואור הוא הספק שלה. בהתאם לכך, ככל שהמחוון הזה גבוה יותר בתחילה עבור נורה, כך היא תצרוך יותר אנרגיה, ותיתן יותר אור.
מכיוון שבמקרה זה יש לא רק תהליך של המרת חשמל למשהו אחר (אור, תרמי וכו'.), אלא גם תהליך התנודה של השדות החשמליים והמגנטיים, מופיע שינוי פאזה בין הזרם למתח, ויש לקחת זאת בחשבון בחישובים נוספים.
כאשר מחשבים את ההספק במעגל זרם חילופין, נהוג להבחין בין רכיבים פעילים, תגובתיים ומלאים.
הרעיון של כוח פעיל
כוח "שימושי" פעיל הוא אותו חלק מהכוח המאפיין ישירות את תהליך המרת האנרגיה החשמלית לאנרגיה אחרת. מסומן באות הלטינית P ונמדד ב וואט (ג').
מחושב לפי הנוסחה: P = U⋅I⋅cosφ,
כאשר U ו-I הם ערך ה-rms של המתח והזרם של המעגל, בהתאמה, cos φ הוא הקוסינוס של זווית הפאזה בין מתח לזרם.
חָשׁוּב! הנוסחה שתוארה קודם לכן מתאימה לחישוב מעגלים עם מתח 220Vעם זאת, יחידות חזקות בדרך כלל משתמשות ברשת עם מתח של 380V. במקרה זה, יש להכפיל את הביטוי בשורש של שלוש או 1.73
הרעיון של כוח תגובתי
כוח "מזיק" תגובתי הוא הכוח שנוצר במהלך פעולתם של מכשירים חשמליים בעלי עומס אינדוקטיבי או קיבולי, ומשקף את התנודות האלקטרומגנטיות המתמשכות. במילים פשוטות, זוהי האנרגיה שעוברת ממקור החשמל לצרכן, ואז חוזרת חזרה לרשת.
כמובן, אי אפשר להשתמש ברכיב זה בעסק, יתר על כן, הוא פוגע ברשת אספקת החשמל במובנים רבים, ולכן הם בדרך כלל מנסים לפצות על כך.
ערך זה מסומן באות הלטינית Q.
זכור! כוח תגובתי אינו נמדד בוואטים רגילים (ג'), ובוולט אמפר תגובתי (Var).
מחושב לפי הנוסחה:
Q = U⋅I⋅sinφ,
כאשר U ו-I הם ערך ה-rms של המתח והזרם של המעגל, בהתאמה, sinφ הוא הסינוס של זווית הפאזה בין מתח לזרם.
חָשׁוּב! בעת החישוב, ערך זה יכול להיות חיובי ושלילי כאחד, בהתאם לתנועת הפאזה.
עומסים קיבוליים ואינדוקטיביים
ההבדל העיקרי בין תגובתי (קיבולי ואינדוקטיבי) עומסים - נוכחות, למעשה, של קיבול והשראות, הנוטים לאגור אנרגיה ובהמשך לתת אותה לרשת.
עומס אינדוקטיבי הופך את האנרגיה של זרם חשמלי תחילה לשדה מגנטי (במהלך חצי מחזור), ולאחר מכן ממיר את האנרגיה של השדה המגנטי לזרם חשמלי ומעביר אותה לרשת. דוגמאות לכך הן מנועי אינדוקציה, מיישרים, שנאים, אלקטרומגנטים.
חָשׁוּב! בעת הפעלת עומס אינדוקטיבי, עקומת הזרם תמיד מפגרת את עקומת המתח בחצי מחזור.
עומס קיבולי הופך את האנרגיה של זרם חשמלי לשדה חשמלי ולאחר מכן ממיר את האנרגיה של השדה המתקבל בחזרה לזרם חשמלי.שני התהליכים נמשכים שוב במשך חצי מחזור כל אחד. דוגמאות לכך הן קבלים, סוללות, מנועים סינכרוניים.
חָשׁוּב! במהלך פעולת עומס קיבולי, עקומת הזרם מובילה את עקומת המתח בחצי מחזור.
גורם כוח cosφ
גורם כוח cosφ (קרא קוסינוס פי) היא כמות פיזיקלית סקלרית המשקפת את היעילות של צריכת אנרגיה חשמלית. במילים פשוטות, מקדם cosφ מראה את נוכחותו של חלק תגובתי ואת הערך של החלק הפעיל שהתקבל ביחס להספק הכולל.
מקדם cosφ נמצא דרך היחס בין הספק חשמלי פעיל להספק חשמלי לכאורה.
הערה! בחישוב מדויק יותר, יש לקחת בחשבון את העיוותים הלא ליניאריים של הסינוסואיד, אולם הם מוזנחים בחישובים קונבנציונליים.
הערך של מקדם זה יכול להשתנות בין 0 ל-1 (אם החישוב מתבצע כאחוז, אז מ-0% ל-100%). מנוסחת החישוב, לא קשה להבין שככל שהערך שלו גדול יותר, כך הרכיב הפעיל גדול יותר, מה שאומר שביצועי המכשיר טובים יותר.
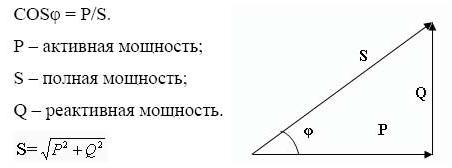
הרעיון של כוח מוחלט. משולש כוח
כוח לכאורה הוא ערך מחושב גיאומטרי השווה לשורש סכום ריבועי ההספק הפעיל והתגובתי, בהתאמה. מסומן באות הלטינית S.
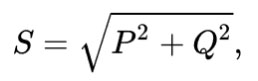
אתה יכול גם לחשב את ההספק הכולל על ידי הכפלת המתח והזרם, בהתאמה.
ס = U⋅I
חָשׁוּב! הספק לכאורה נמדד בוולט-אמפר (VA).
משולש הכוח הוא ייצוג נוח של כל החישובים שתוארו קודם לכן והקשרים בין כוח פעיל, תגובתי ונראה לעין.
הרגליים משקפות את הרכיבים התגובתיים והפעילים, התחתון - הכוח הכולל. על פי חוקי הגיאומטריה, הקוסינוס של הזווית φ שווה ליחס בין הרכיבים הפעילים לסך הכל, כלומר, הוא גורם ההספק.
כיצד למצוא כוח פעיל, תגובתי ונראה לעין. דוגמא חישוב
כל החישובים מבוססים על הנוסחאות שהוזכרו לעיל ומשולש הכוח. בואו נסתכל על הבעיה שבה נתקלים לרוב בפועל.
בדרך כלל, מכשירי חשמל מסומנים עם הספק פעיל וערך מקדם cosφ. בעזרת נתונים אלה, קל לחשב את הרכיבים התגובתיים והסך הכל.
לשם כך, נחלק את ההספק הפעיל במקדם cosφ ונקבל את המכפלה של זרם ומתח. זה יהיה מלא כוח.
יתרה מכך, בהתבסס על משולש העוצמה, אנו מוצאים את הכוח התגובתי שווה לריבוע ההפרש בין ריבועי העוצמה הנראית לעין והפעילה.
כיצד נמדדת cosφ בפועל
הערך של מקדם cosφ מצוין בדרך כלל על התגים של מכשירי חשמל, אולם אם יש צורך למדוד אותו בפועל, הם משתמשים במכשיר מיוחד - מד פאזה. כמו כן, מד וואטים דיגיטלי יכול להתמודד בקלות עם משימה זו.

אם מקדם cosφ המתקבל נמוך מספיק, אז ניתן לפצות אותו באופן מעשי. זה נעשה בעיקר על ידי הכללת התקנים נוספים במעגל.
- אם יש צורך לתקן את הרכיב התגובתי, יש לכלול אלמנט תגובתי במעגל, הפועל בניגוד למכשיר שכבר מתפקד. כדי לפצות על פעולתו של מנוע אינדוקציה, למשל עומס אינדוקטיבי, מחובר קבל במקביל. אלקטרומגנט מחובר כדי לפצות את המנוע הסינכרוני.
- אם יש צורך לתקן בעיות לא-לינאריות, מתקן cosφ פסיבי מוכנס למעגל, למשל, זה יכול להיות משנק השראות גבוה המחובר בסדרה עם העומס.
כוח הוא אחד האינדיקטורים החשובים ביותר של מכשירי חשמל, אז לדעת מה זה וכיצד הוא מחושב שימושי לא רק עבור תלמידי בית ספר ואנשים המתמחים בטכנולוגיה, אלא גם עבור כל אחד מאיתנו.
מאמרים דומים: